We come spinning out of nothing,
scattering stars like dust!
~Jalāl ad-Dīn Muhammad Rūmī

Last week, I explained Rayleigh and Raman scattering from a classical point of view. In the process, I explained why the sky is blue and introduced Raman spectroscopy, a powerful tool for studying the structure of molecules. This week, I fill in the gaps and explain scattering from a quantum-mechanical point of view.
Before we can talk about scattering, though, we need to review some important ideas from quantum mechanics: energy levels and the Heisenberg uncertainty principle.
Energy Levels
The story of energy levels starts deep within the atom. I’ve previously discussed the fact that particles are waves and how this means that electrons can only have certain specific energies inside an atom. The energy and momentum of a particle control how many times the corresponding wave wiggles within a certain distance. As shown below, these wiggles (wavelengths) must fit in a circle around the nucleus of the atom–the electron can’t cut off its oscillation halfway through to fit itself into an orbit!

If the atom is part of a molecule (especially a crystal), the discrete allowed energies become so numerous that, together, they look like a continuous band. And this leads to band structure.
For clarity, physicists often imagine extremely simple atoms with only two or three allowed electron orbits, each of which is allowed only at a single specific energy and a single specific momentum. Depending on the situation, they even neglect the momenta and only look at the allowed energies. This is what we’ll do. For example, the figure below shows a two-level atom with a single electron in the lowest energy state.

When a photon—a light particle–hits the atom (or, alternatively, passes right through it), it has the potential to affect the electron. If we ignore quantum mechanics and look at this classically, the light would always accelerate the electron, since the electron is a charged particle and electromagnetic fields affect charged particles.
However, if the electron accelerated, it would gain kinetic energy. This gain is only allowed if the electron ends up with one of the allowed energies–and if the electron is accelerated, it will absorb the photon’s energy and momentum. So it can only absorb the photon if the electron’s new energy and momentum are allowed within the atom. Otherwise, surprisingly, the photon passes right through the atom unmolested, as shown below.

Right: A photon with the wrong energy and momentum (blue) hits the atom. The electron (yellow) is unable to absorb the photon because the electron’s new energy and momentum would not be allowed, so the photon passes through unmolested.
Importantly, once an electron absorbs a photon, it can sit in the higher energy level as long it likes. It’s under no obligation whatsoever to drop down to a lower energy level state.
(Astute regular readers may complain here. In the past, I said that electrons want to be in the lowest-energy state available. Both statements are true. In the idealized situation, electrons stay in whatever energy state they’re currently in unless provoked by a photon. But in the real world, electrons drop to lower-energy states through fluorescence. This is because, in the real world–thanks to quantum field theory–there are always photons or other particles for the electron to interact with. And these other particles allow the electron to drop down to lower energy levels through stimulated emission.)
Uncertainty
There’s a lot to say about Werner Heisenberg’s famous uncertainty principle…and I have said a fair amount in the past. For now, though, we’ll be brief. The uncertainty principle is a consequence of the fact that matter is both a particle and a wave. If you’ve heard of it, you probably know what it says:
![]()
or, in English,
We cannot know both the position and the momentum of a particle at the same time. In other words, we can’t precisely know where a particle is and how fast it’s going at the same time.
And this is true, but it’s not useful for us. We’d rather restate the uncertainty principle equivalently as
![]()
or, in English,
Over short times, we cannot precisely know the energy of a particle. Only if we wait long enough can we accurately measure its energy.
The consequences of this restatement are a little nuts. Written this way, the uncertainty principle tells us that a particle can have enormous energy, so long as it has that energy for only a short time. Perhaps more importantly, if the electron is in an atom or molecule, that enormous energy doesn’t have to be quantum-mechanically allowed.
(I know the uncertainty principle seems crazy and unintuitive. There are a few helpful thought experiments that I’ll try to write about in the future.)
Virtual Energy Levels
This means that I fed you a little white lie earlier. I told you that an electron in an atom (or molecule) won’t absorb a photon if that photon has the wrong energy. But this isn’t quite true. The electron can absorb the photon, so long as it doesn’t keep the photon’s energy for long.
In this case, an electron jumps up into a so-called “virtual energy state,” which can only exist for short times thanks to the uncertainty principle. Then, before the uncertainty principle is violated, the electron emits a photon in a random direction, allowing it to drop back down to its original allowed energy state.

Because the energy difference between the virtual state and the original state is equal to the energy of the absorbed photon, the electron must vent precisely that amount of energy. So it emits a photon of the same energy–and thus color–as the original photon.
Wait…a photon is absorbed and then re-emitted in a random direction? Those of you who read last week’s post know that that’s Rayleigh scattering! Thus, this is the quantum-mechanical description of how light bounces off of an atom or molecule. (Important note: the description is a bit different for metals, which are reflective.)
Just to tie everything together with last week: In the classical picture, we treat a photon as a wiggling electromagnetic field, which causes our electron to wiggle in its orbit around the atom (or molecule). Although this uses up the photon’s energy, the wiggling electron then recreates the photon traveling in a random direction. In the quantum picture, the electron absorbs the photon, jumps up to a virtual energy level that’s allowed only by the uncertainty principle, then drops back down to its original energy level, emitting a new photon of the same color in a random direction.

Enter Raman
But, as we discussed last week, things are a little different if light scatters off of a molecule. In an atom, electrons are localized to one nucleus. In a molecule, the electrons have several atoms to roam across. (As I discussed in my post on bonding, atoms in a molecule share electrons.) But atomic bonds in molecules are not static things. Because of the heat in the molecule, the atomic bonds wobble and vibrate all on their own.
This wobbling of the atomic bonds not only contributes to the kinetic energy of the electrons, but acts as an additional allowed energy level for the electron. So if we place our two-level atom (above) into a molecule, it will then have three levels (below): two atomic energy levels and one kinetic energy level that comes from the vibration of the molecule. Usually the vibrational state is at a much lower energy than the atomic excited states.

Now, when a particle absorbs a photon with the wrong energy and jumps up into a virtual excited state, it can drop down into either the vibrational excited state or the ground state, as shown below. But since the vibrational excited state has more energy than the ground state, the particle needs to vent less energy if it drops into the vibrational state. This means that it will emit a photon with less energy–i.e., a different color! This is called Stokes scattering.

Of course, an electron might start higher than the ground state–say, in the vibrational excited state. Then, when it absorbs the photon and jumps into the virtual energy state, it could drop past where it started, into an even lower energy state. In this case, the emitted photon would have more energy than the absorbed photon. This is called anti-Stokes scattering.

Both Stokes scattering and anti-Stokes scattering are examples of Raman scattering, which I explained from a classical point of view last week.
Why Two Viewpoints?
You may ask why I bothered explaining this phenomenon twice–once from a classical point of view and one from a quantum point of view. Well, both have their advantages. The classical viewpoint is undoubtedly more accessible. However, the quantum viewpoint is more accurate and, in general, more powerful in terms of making useful calculations. When we describe physical systems, scattering can quickly get insanely complicated, since the structure of any given molecule is often insanely complicated. The easiest way is to use the quantum picture of scattering and let the band structure of the material supply the allowed energy levels. When you do that, you can’t ignore momentum.
One reason I personally discussed both descriptions is that I’d like you, my readers, to see how the classical and quantum pictures correspond–how they’re the same and how they’re different. And, well…scattering is just fun! 🙂
Further Reading
You may find the following articles I’ve written helpful.
- My first article on scattering
- My article on particle wave duality
- My article on the Bohr model of the atom
- My article on the interpretation of matter waves
- My article on Fourier transforms/series and the Heisenberg uncertainty principle
- My article on atomic bonds
- My article on band theory
- My article on laser physics
Other Resources
Raman scattering is a pretty esoteric topic, so all the resources this time are pretty technical. The best I could find are some lecture slides from various universities:
- Here’s a nice, short, technical introduction to Raman scattering.
- For the brave, here is a mathematical treatment of Rayleigh scattering.
- Here are some lecture slides.
- Some more lecture slides.
- Hyperphysics has a brief description here.
- My introduction to this topic came from the excellent “Introductory Raman Spectroscopy” by Ferraro et al.
- My undergraduate physics honors thesis has a chapter on Raman scattering.
Questions? Comments? Insults?
As always, if you have any questions, comments or corrections–or if you just want to say hi–please drop me a line.

Great explanation of scaterring in quantum mechanics. But i have one question, because i cant puzzle it out. I know that one out of million or even more photons scatter like Raman. But why is that? I
Thanks for reading, Grega! There are a number of ways to think about this. Perhaps the easiest explanation comes from the pseudo-classical approximation of Raman scattering I talked about before (https://en.wikipedia.org/wiki/Diffuse_sky_radiation). In the pseudo-classical picture, Raman scattering happens when we polarize a molecule and the wobbling of the polarized charges due to the thermal motion of the molecule interacts with the light.
But for the molecule to become polarized, it has to already be affected by the incoming light! This means that Rayleigh scattering happens first, before any Raman scattering can take place. It gets all the choice bits of bright light, if you will.
If we want to explain this discrepancy from the quantum perspective, we have to take more quantum mechanics into account than I did in my article. In this article, I ignored the fact that with each energy level an electron is allowed to inhabit, there is a unique momentum it’s allowed to inhabit. And this momentum will be different for a vibrational energy state than it would be for an “atomic” energy state of the same energy. But photons carry a specific amount of momentum—always the same amount. So if an electron is excited out of an atomic energy level into a virtual energy state, the momentum condition usually forbids it from falling into the vibrational energy state that would result in Raman scattering.
It can only fall into the vibrational energy state because of the Heisenberg Uncertainty principle, which blurs everything.
Does this help?
Thank you for the answer and it is more clearer now.
Thanks for the post! It is all right apparently, but what troubles me in this quantum picture of Rayleigh scattering is that it looks like a spontaneous process, whereas classically scattering is fundamentally a stimulated process induced by the incident wave.
And secondly if the virtual level is very short-lived it follows that it must have a great energy uncertainty. How come the emitted photon has exactly the same frequency, then?
And lastly, do you think “rayleigh_review.png” would look better without the vertical arrows from the atom? Apparently it does not scatter in those directions..
Thanks for your comments, Anton. Regarding your questions:
1. Quantum scattering is also a stimulated process. This is because if there is no incident light, the scattering molecule is in a low energy state. It will not emit unless it is excited by an incident wave.
2. The virtual level is indeed short-lived. But energy must be conserved. The uncertainty comes in from the fact that the virtual level exists at all! It is forbidden by the selection rules of the quantum system but it exists anyway, thanks to the uncertainty principle.
3. Ah, that’s not true. It’s possible for light to be Rayleigh scattered perpendicularly. The intensity is simply lower. It follows this formula:
https://en.wikipedia.org/wiki/Rayleigh_scattering#From_molecules
where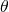 is the angle.
is the angle.
———————–
3. Ah, that’s not true. It’s possible for light to be Rayleigh scattered perpendicularly. The intensity is simply lower. It follows this formula:
https://en.wikipedia.org/wiki/Rayleigh_scattering#From_molecules
———————–
Oh, I see! It’s just that the incident light is unpolarized. The formulas in Wikipedia obviously apply to that case. So we have electric field (as well as atomic charges) oscillating both in plane and out of plane of the picture, in which case there is scattering in the perpendicular direction but half as much as longitudinally.
Not so sure about the first statement though.. By this logic, optically excited spontaneous emission (like fluorescence) is also a “stimulated” process whereas it is fundamentally different from stimulated emission. For example, the spectrum of spontaneous emission is centered at the transition frequency and does not depend strongly on the spectrum of the exciting light, while Rayleigh scattering is spectrally identical to it.
Thanks for the great summary. In the classical description of Rayleigh scattering the intensity of the scattering varies with the wavelength of the incident light. This explains why the sky is blue: Blue light scatters better than red light. How do you describe this in the quantum mechanical description?