
I recently posted an article on Kaluza-Klein theory. This was partly because I was working a paper on it as a final project in my second semester of general relativity. The paper is finished, and I thought I’d upload it for the more mathematically inclined of my readers. If you’re interested, you can find it here.

Thanks for publishing this, it is very useful now that I need to learn about Kaluza-Klein reduction for my thesis. I’m stuck defining the curvature form, isn’t it d\omega + \omega \wedge \omega with everything hatted? In particular, I don’t understand why the third term \omega\wedge e, is of this form. Could the fact that the manifold comprises two disjoint ones, M^4\times M^1 be related? If so, how is the spin connection decomposed in such a manifold?
Hey Peter, I’m glad I could help! As you guessed, I’m taking advantage of the fact that the manifold can be decomposed. I think you actually caught a typo in that line. The index c should run only from 0 to 3.
RIght, in five dimensions, it’s
\hat{R} = d\hat{\omega} + \hat{\omega} \wedge\hat{omega}
So what I’ve done is decomposed my last \hat{\omega}, \hat{\omega}^c_{\ b} into the four dimensional one plus an additional term:
\hat{R} = d\hat{\omega} + \hat{\omega}^A_c \wedge\hat{\omega}^c_B + \hat{omega}^A_z \wedge\hat{\omega}^z_B
Then I’m just using how the spin connections are defined. Recall that
\omega^a_b = \omega_\mu^a_b dx^\mu
if you wedge the five dimensional one with the four dimensional one in the z direction, e^z pops out.
Hope this helps!
The definition of the spin connection I know is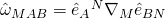 , is this what you mean?
, is this what you mean?
I assume that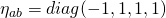 ,
, 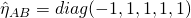 . Then,
. Then, 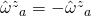 only if
only if 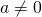 , otherwise it equals
, otherwise it equals 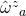 , right? But if this is so, shouldn’t
, right? But if this is so, shouldn’t 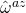 depend on whether
depend on whether 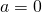 or not?
or not?
Thanks for your help, it is much appreciated. I’ve been able to do most of the calculations, but I’m still stuck with these problems.
I meant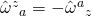 for
for 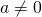 and
and 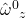 otherwise.
otherwise.
Oh sorry, yes. I had a brain fart. All I meant was that if you wedge a unit one form e_A with itself in the “tetrad” basis, it goes to zero. So if you wedge a five-dimensional spin connection with a four-dimensional one, the four e_a one-forms cancel with themselves, leaving just e_z and the component of the spin connection multiplying it.
Also sorry for taking so long to get back to you. I’m at a summer school at the moment, and as you probably know, those are pretty intense.
(I also apologize in advance if I say something very wrong. It’s been about a year since I’ve thought about Kaluza-Klein stuff!)
Hi Jonha, great effort!
I am also following Pope in his example, however as he has left out the details from spin-connection to the curvature I was pleased to see that someone like yourself has taken the time to go through it in a little more detail.
However, firstly I cannot make sense of your decomposition in the Cartan structure equations, and secondly, the one calculation that you have done for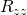 seems rather spooky. What do I mean, well, take a look at your dilaton term (
seems rather spooky. What do I mean, well, take a look at your dilaton term (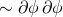 ) in (23) clearly this vanishes since you are taking the wedge product between
) in (23) clearly this vanishes since you are taking the wedge product between 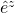 and itself, no?
and itself, no?
Also, I fail to see how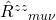 is what determines
is what determines 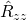 , obviously you need more terms?
, obviously you need more terms?
So you also need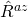 .
.
… fail to see how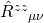 …
…
Hi Isak,
I’m sorry for not responding earlier… somehow I missed your comment! I haven’t looked at this paper in a long time. Are you still stuck? If so, I’ll try and go back through my derivation.